Doublet
En optique, un doublet est l'association de deux lentilles pour former un dispositif optique. On le caractérise le plus souvent par la position des centres optiques des lentilles.

Catégories :
Lentille - Optique appliquée à la photographie - Technique photographique - Technique cinématographique
Recherche sur Google Images :

Source image : www.astrosurf.com Cette image est un résultat de recherche de Google Image. Elle est peut-être réduite par rapport à l'originale et/ou protégée par des droits d'auteur. |
Page(s) en rapport avec ce sujet :
- Un doublet est constitué de deux lentilles minces non accolées.... On montre (voir votre cours d'optique) que : La distance focale image est f'= - f'1. f... (source : univ-lemans)
- Correction de la partie 6 du TD " Lentilles minces".... 6.1 Le foyer image F i du doublet est l'intersection avec l'axe optique du rayon émergent... (source : books.google)
- ) Le plan principal image [H'] du doublet est obtenu à partir de la... est réfracté par cette lentille parallèlement à l'axe optique, suivant (11).... (source : membres.lycos)
En optique, un doublet est l'association de deux lentilles pour former un dispositif optique. On le caractérise le plus souvent par la position des centres optiques des lentilles. Ce type d'association sert à modéliser et de comprendre le fonctionnement d'un particulièrement grand nombre d'instruments d'optique.
Doublet accolé
On parle de doublet accolé quand les centres optiques des deux lentilles sont confondus. Dans ce cas la longueur focale f'du doublet est donnée, si on nomme f'1 et f'2 les longueurs focales des deux lentilles, par :
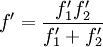
Formules
On nomme S1 et S2 les positions des centres optiques des lentilles et s2 = S1S2 la distance les séparant.
Le point B a pour image le point Bi, qui sert lui-même d'objet à la lentille 2, qui en fait une image finale Bi2 Les deux formules de base sont :
- ƒo / x + ƒi / xi = 1
dite de Descartes, et celle donnant le grandissement
- Γ = yi / y.
Elles peuvent s'écrire sous la forme :
et
Ces formules permettent de construire l'image Bi par la détermination par le calcul algébrique de ses coordonnées xi et yi à partir des coordonnées x et y d'un point objet B.
Points principaux d'un doublet
Sur la figure ci-dessous, l'objet B est sur une droite parallèle à l'axe Ox (y est constant), qui coupe la première lentille en un point I. Son image B'1 est sur la droite IF'1.
- B, O1 et B'1 sont alignés puisque les rayons passant par O1 ne sont pas déviés.
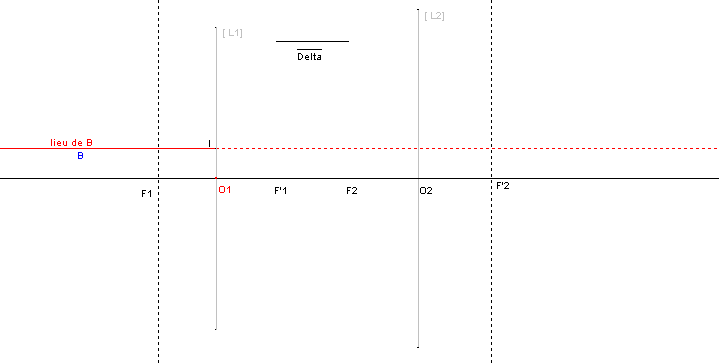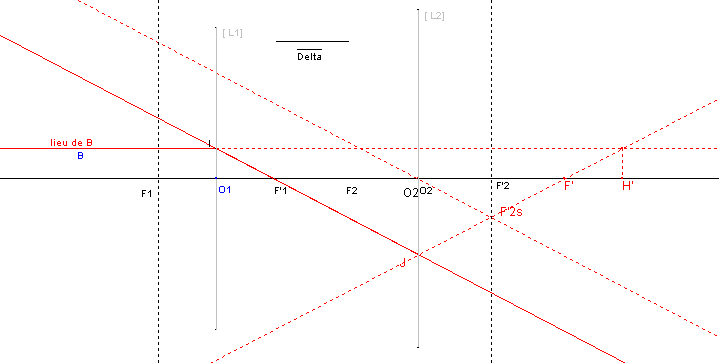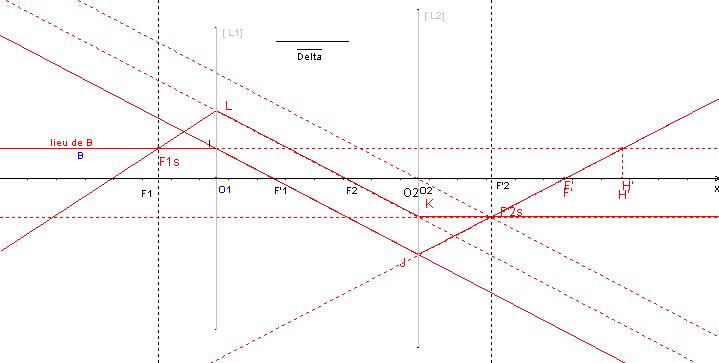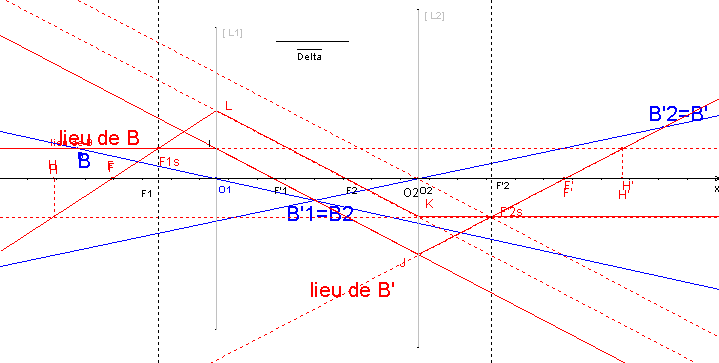
Le point B'1 sert alors d'objet à la seconde lentille en utilisant les mêmes formules avec évidemment en prenant comme origine l'abscisse O2 de la seconde lentille ; l'image finale B' se trouve sur la droite JF' 2s où J est l'intersection de IF'1 avec la seconde lentille.
- B'1, O2 et B' 2 sont alignés puisque les rayons passant par O2 ne sont pas déviés.
Reste à constater que le lieu de l'image finale B'2 est une droite passant par F', foyer image de la totalité, et que ce point F' est l'image du foyer image F' 1 de la première lentille par la seconde lentille, soit selon la formule de Newton vérifiant :
- F2F' 1 × F' 2F' = ƒ2 × ƒ'2
Notons au passage que le foyer objet F du doublet a pour image par la première lentille le foyer objet F2 de la seconde lentille, ce qui s'écrit :
- F 1F × F' 1F2 = ƒ1 × ƒ'1
F1 foyer objet de la première lentille a pour image par la totalité du doublet le foyer image de la seconde lentille F' 2 ; ceci s'écrit :
- FF 1 × F'F' 2 = - ƒ1 · ƒ'1 · ƒ2 · ƒ'2 / (F' 1F2) 2 = ƒ1 · ƒ2 / F' 1F2 × ƒ'1 · ƒ'2 / F2F' 1
C'est avec ces formules qu'on peut vérifier la position des points dits cardinaux sur la figure ci-dessous.
Figures géométriques
Ci-dessous une animation où en gris sont représentées les lentilles minces. L'animation montre, par la construction géométrique :
- en rouge : comment procéder pour trouver les foyers et plans principaux du doublet.
- puis en bleu : comment trouver l'image B'finale en trouvant en premier lieu B'1 produit par L1 et qui sert d'objet pour L2.
Applications
- Microscope optique
- Lunette astronomique
- Lunette de Galilée
- Longue-vue
- Jumelles
Voir aussi
|
Recherche sur Amazone (livres) : |
Voir la liste des contributeurs.
La version présentée ici à été extraite depuis cette source le 14/04/2009.
Ce texte est disponible sous les termes de la licence de documentation libre GNU (GFDL).
La liste des définitions proposées en tête de page est une sélection parmi les résultats obtenus à l'aide de la commande "define:" de Google.
Cette page fait partie du projet Wikibis.
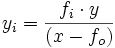

 Accueil
Accueil Recherche
Recherche Début page
Début page Contact
Contact Imprimer
Imprimer Accessibilité
Accessibilité