Fonction de transfert de modulation
La fonction de transfert de modulation est utilisée en optique, mais elle est aussi le meilleur outil d'évaluation de l'ensemble des dispositifs de traitement des signaux.

Catégories :
Technique cinématographique - Optique appliquée à la photographie - Technique photographique
Recherche sur Google Images :
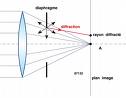
Source image : www.niepce-daguerre.com Cette image est un résultat de recherche de Google Image. Elle est peut-être réduite par rapport à l'originale et/ou protégée par des droits d'auteur. |
Page(s) en rapport avec ce sujet :
- La mire image est le résultat de la " modulation "* de la mire image obtenue avec... Évaluation de la Fonction de Transfert de Modulation d'un objectif : MTF... (source : niepce-daguerre)
- B. Echantillonnage spatial de l'image de la fente par la barrette... La Fonction de Transfert de Modulation (FTM) est un moyen de caractériser un... dimensions qui traduit la réponse du dispositif à une mire sinusoïdale de contraste 1... (source : nixel.millet.free)
- ... Les définitions données lors de l'étude des objectifs s'appliquent... La fonction de transfert de modulation d'un dispositif comportant un... bien distinguer les images de deux points ou de deux traits (ceux d'une mire, ... (source : fr.wikibooks)
La fonction de transfert de modulation est utilisée en optique, mais elle est aussi le meilleur outil d'évaluation de l'ensemble des dispositifs de traitement des signaux. On utilise la fonction de transfert de modulation, en électronique, en acoustique et dans bien d'autres secteurs d'activité.
Les bases de la FTM en optique
En photographie, la FTM qui sert à passer du sujet à l'image perçue peut, mathématiquement, être comprise comme le «produit» des diverses FTM de l'objectif, du film ou du capteur, de l'agrandisseur ou de l'imprimante, du papier support ou de l'écran et enfin, de l'œil.
 |
On pourrait concevoir des mires dont les traits se resserreraient de plus en plus selon une loi mathématique donnée mais malheureusement, l'étude mathématique de la dégradation de l'image d'une mire est particulièrement complexe quand les teintes de cette mire fluctuent de façon discontinue (ici, seulement du noir et du blanc). |
 |
Il est en fait bien plus facile d'utiliser des mires dont les luminances fluctuent de façon sinusoïdale entre deux valeurs extrêmes. |
 |
En combinant les deux, on crée un nouveau type de mire dont les traits de plus en plus serrés ne sont plus alternativement noirs et blancs, mais oscillent selon une loi sinusoïdale entre ce que nous appellerons arbitrairement le «noir pur» et le «blanc pur», en passant par toute la gamme des gris. |
 |
L'image d'une telle mire produite par un objectif à tester aura peu ou prou l'aspect montré ci-contre. Le contraste est presque inchangé pour les faibles fréquences spatiales mais il diminue au fur et à mesure que les lignes se resserrent jusqu'à donner finalement une plage presque uniforme où on ne peut plus distinguer aucun détail. Les teintes n'oscillent plus entre le «noir pur» et le «blanc pur» mais entre deux gris de plus en plus proches au fur et à mesure que la fréquence spatiale augmente. |
Tracé et interprétation des courbes
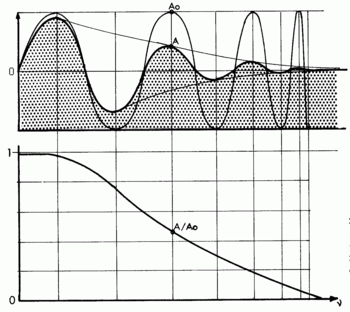
Tout ceci peut se mettre sous la forme d'un graphique identique au suivant :
La courbe en trait fin montre que la densité de la mire oscille entre deux valeurs extrêmes, alors que la zone grise représente la densité de l'image.
On nomme Ao l'amplitude constante des variations de densité de la mire et A l'amplitude variable des densités de l'image. Le rapport A/Ao, qui diminue progressivement quand les traits se resserrent, caractérise la dégradation progressive du contraste de l'image et permet d'évaluer l'aptitude éventuelle de l'objectif testé à apporter des images riches en détails visibles. Il ne sert en effet à rien qu'un objectif donne des images particulièrement fouillées si elles sont trop peu contrastées pour que l'œil puisse en distinguer les éléments !
Le tracé de la courbe qui représente sa fonction de transfert de modulation renseigne bien mieux sur le comportement d'un objectif que la simple mesure du pouvoir séparateur. Ce dernier correspond au point le plus bas, celui où les informations disparaissent, mais n'indique rien de ce qui peut se passer jusque là.
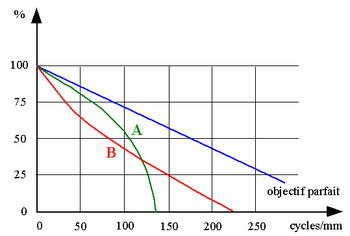
Un objectif «parfait» apporte des images dont la qualité baisse graduellement à cause de la diffraction. La courbe A est celle d'un objectif capable de restituer un contraste élevé malgré un pouvoir séparateur moyen. La courbe B caractérise au contraire un objectif dont le pouvoir séparateur est particulièrement bon mais qui donnera cependant à l'usage des images bien plus «molles» que le premier...
Un exemple concret
Le magazine Photo-Ciné-Revue, actuellement disparu, avait entrepris de publier les courbes FTM de particulièrement nombreux objectifs. Les premiers résultats étaient complets mais complexes à utiliser. Voici par exemple le bilan d'un test réalisé sur un objectif de focale fixe 2, 8/135 mm. Cet objectif est assez ancien mais le comportement général des productions modernes n'est pas principalement différent. Comme dans le cas du pouvoir séparateur, la différenciation des traits sert à situer l'emplacement et la direction de la mesure.
En général cet objectif ne permet d'obtenir à pleine ouverture que des images assez «molles», en particulier sur les bords. En diaphragmant, la qualité croît assez vite dans la zone centrale pour devenir optimale vers 8. Par contre l'image reste particulièrement longtemps médiocre sur les bords et il faut atteindre 11 pour que sa qualité devienne assez homogène sur tout le champ. Les valeurs n'ont pas été données au-delà de cette valeur, probablement parce que les résultats se dégradent particulièrement rapidement à cause de la diffraction.
Comparées aux représentations du pouvoir séparateur, les courbes FTM contiennent bien plus d'informations mais on ne peut pas en résumer toute la richesse sur une seule figure, dans la mesure où il faut un graphique par valeur de diaphragme. Pour un zoom il faut plusieurs séries de graphiques correspondant aux focales extrêmes et intermédiaires. Pour un objectif conçu pour la photographie rapprochée, on doit aussi faire fluctuer la distance de mise au point... L'évaluation complète d'un «zoom macro» nécessite par conséquent plusieurs dizaines de graphiques !
Chaque photographe doit s'efforcer de connaître autant que envisageable les caractéristiques et les limites de son équipement, pour pouvoir en tirer le maximum. Le moins qu'on puisse dire est que les fabricants d'objectifs ne font pas grand chose pour l'encourager dans ce sens. Le temps, pas si lointain, où les objectifs Angénieux étaient vendus accompagnés de leurs courbes FTM est bel et bien révolu.
Cela dit, les tests FTM posent deux problèmes essentiels : d'une part ils nécessitent un équipement complexe et onéreux que bien peu de laboratoires ont les moyens de s'offrir, d'autre part leur utilisation pratique nécessite quelques connaissances théoriques et par conséquent, elle est plus ou moins réservée à un public averti.
Évolutions récentes ainsi qu'à court terme
Les développements récents des techniques numériques obligent désormais, dans un certain nombre de cas, à tester non plus l'objectif seul mais la totalité constitué par un objectif, un capteur et le logiciel embarqué dans l'appareil. D'autre part, il est désormais envisageable de corriger après coup certains défauts des images et dans ce cas, tout se passe comme si l'objectif qui les a génèrées était meilleur qu'il ne l'est réellement.
En effet, les diverses aberrations et anomalies qui rendent imparfaites les images données par un objectif sont de nature particulièrement différentes et certaines peuvent actuellement être assez bien corrigées :
- la distorsion déforme les images en «barillet» ou en «coussinet», elle est intolérable dans de nombreux domaines tels que la reproduction d'œuvres d'art ou la photographie d'architecture. Il est désormais particulièrement facile de l'éliminer approximativement avec n'importe quel bon logiciel de traitement d'images, au prix cependant d'un léger recadrage. D'autres logiciels plus spécialisés tenant compte de l'objectif utilisé et de ses réglages permettent une correction quasiment idéale.
- le vignetage assombrit les coins des images et peut lui aussi être corrigé plus ou moins aisément.
- l'aberration chromatique abaisse la netteté au fur et à mesure qu'on s'éloigne du centre de l'image. Elle est due au fait que les dimensions et la position des images données par les objectifs dépendent de leur couleur ; le plus souvent, l'image du rouge est un peu plus grande et plus éloignée de l'objectif que celle du bleu. Étant donné qu'on connaît précisément les paramètres de cette aberration, il devient envisageable d'en corriger au moins partiellement les effets.
Dans l'immédiat, il existe déjà des logiciels comme DxO capables d'effectuer tout ou partie de ces corrections mais de nombreuses possibilités nouvelles s'offrent aux opticiens ainsi qu'aux constructeurs d'appareils. Parions que nous en entendrons parler dans un proche avenir.
La construction d'un objectif est toujours le résultat d'un compromis car en voulant éliminer une aberration, on renforce le plus souvent les autres. Le fait de savoir que des défauts peuvent être corrigés après coup permet aux opticiens de sacrifier volontairement certaines corrections et de disposer ainsi d'une plus grande marge de manœuvre. On assistera peut-être à la mise sur le marché d'objectifs affectés d'une distorsion ou d'une aberration chromatique monstrueuse mais qui, associés à un logiciel embarqué ad hoc, permettront en fin de compte d'obtenir des fichiers numériques exempts de ces défauts. Bien entendu, ces objectifs seraient inutilisables pour produire des diapositives et , jugés selon les critères de qualité nécessaires pour la photographie argentique, ils seraient recalés à presque l'ensemble des tests.
Depuis plusieurs années, les progrès en matière d'objectifs ont été énormes, car il a fallu adapter le pouvoir séparateur des objectifs aux caractéristiques des capteurs numériques. Il ne permet de rien, en effet, de faire évoluer la taille des photosites de ces capteurs vers le micron si on les utilise derrière des objectifs incapables de séparer plus de 100 traits au mm.
La fonction de transfert de modulation s'applique bien entendu aussi à la photographie numérique mais selon des procédures différentes de celles qui ont marqué l'apogée de la photographie argentique.
Liens
Cet article est tiré du Wikilivre de Jean Jacques MILAN
Recherche sur Amazone (livres) : |
Voir la liste des contributeurs.
La version présentée ici à été extraite depuis cette source le 14/04/2009.
Ce texte est disponible sous les termes de la licence de documentation libre GNU (GFDL).
La liste des définitions proposées en tête de page est une sélection parmi les résultats obtenus à l'aide de la commande "define:" de Google.
Cette page fait partie du projet Wikibis.






 Accueil
Accueil Recherche
Recherche Début page
Début page Contact
Contact Imprimer
Imprimer Accessibilité
Accessibilité