Lentille épaisse

Une lentille épaisse est une lentille dont l'épaisseur n'est pas négligeable devant les rayons de courbure de ses faces.

Catégories :

Lentille - Optique appliquée à la photographie - Technique photographique - Technique cinématographique

Source image : www.jmbprofessionnel.org
Cette image est un résultat de recherche de Google Image. Elle est peut-être réduite par rapport à l'originale et/ou protégée par des droits d'auteur.

Page(s) en rapport avec ce sujet :

Une lentille épaisse est une lentille dont l'épaisseur au centre n'est pas faible devant les rayons de courbure de ces faces.... figure Cabri pour la construction de l'image d'un point par une lentille épaisse... (source : spc.ac-aix-marseille)
Une lentille épaisse est un dispositif centré constitué de deux dioptres (dont au... focale distance image foyer objet foyer. ) dpt. () e postérieur face... (source : books.google)
L'image formee par la face d'entree sert d'objet pour la face de sortie et son...... Une lentille epaisse est formee par deux surfaces spheriques... (source : springerlink)

Une lentille épaisse est une lentille dont l'épaisseur n'est pas négligeable devant les rayons de courbure de ses faces. Les lentilles épaisses n'ont pas les mêmes propriétés que les lentilles minces. Les foyers focaux sont surtout définis à partir des plans principaux. Qui plus est les distances focales objet et image ne sont généralement pas identiques.

Formules de conjugaison

On considère une lentille d'indice n dans l'air (indice 1). Soit S₁ l'intersection de la face d'entrée avec l'axe optique, S₂ l'intersection de la face de sortie avec l'axe optique, R₁ le rayon de la face d'entrée et R₂ le rayon de la face de sortie, on peut montrer que dans les conditions de Gauss :

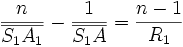
$\frac{n}{\overline{S_1A_1}}- \frac{1}{\overline{S_1A}}=\frac{n-1}{R_1}$

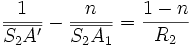
$\frac{1}{\overline{S_2A'}}- \frac{n}{\overline{S_2A_1}}=\frac{1-n}{R_2}$

où A₁ est l'image de A par le dioptre constitué par la face d'entrée et A'l'image de A₁ par le dioptre constitué par la face de sortie : A'est par conséquent l'image de A par la lentille.

Dans le cas d'une lentille mince, S₁ et S₂ sont presque confondus avec le centre optique et :

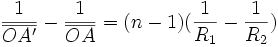
$\frac{1}{\overline{OA'}}- \frac{1}{\overline{OA}}=(n-1)(\frac{1}{R_1}-\frac{1}{R_2})$

On retrouve alors la formule de conjugaison de Descartes avec 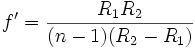$f'=\frac{R_1R_2}{(n-1)(R_2-R_1)}$

Voir aussi

Recherche sur Amazone (livres) :

Ce texte est issu de l'encyclopédie Wikipedia. Vous pouvez consulter sa version originale dans cette encyclopédie à l'adresse http://fr.wikipedia.org/wiki/Lentille_%C3%A9paisse.
Voir la liste des contributeurs.
La version présentée ici à été extraite depuis cette source le 15/04/2009.
Ce texte est disponible sous les termes de la licence de documentation libre GNU (GFDL).
La liste des définitions proposées en tête de page est une sélection parmi les résultats obtenus à l'aide de la commande "define:" de Google.
Cette page fait partie du projet Wikibis.