Méthode de Silbermann

La méthode de Silbermann est une méthode focométrique de détermination expérimentale de la focale d'une lentille optique convergente.

Principe

On considère une lentille mince convergente de focale f', de centre O, de foyers image F'et objet F.

Soit D, la distance entre l'objet A (sur l'axe optique) et l'écran (où on visualise l'image A'). Si la lentille est à mi-distance entre l'objet et l'écran, on peut déduire la valeur de la focale f'par la formule :

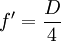
$f'=\frac{D}{4}$

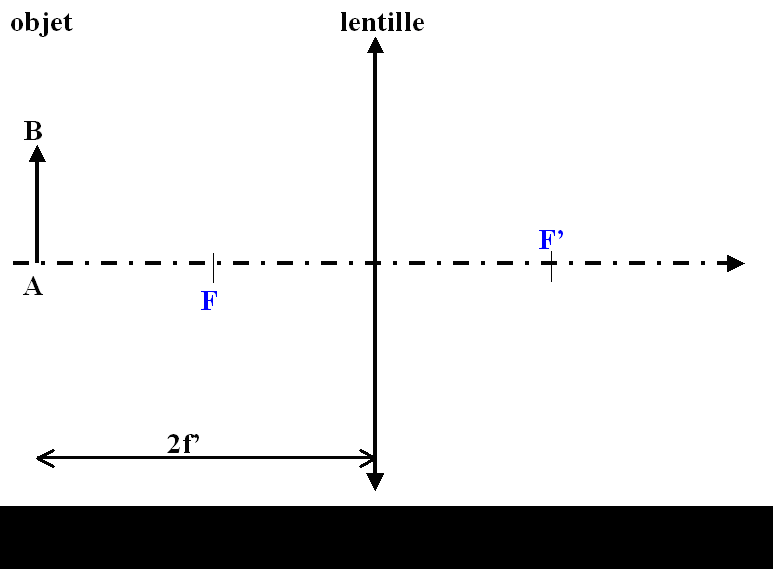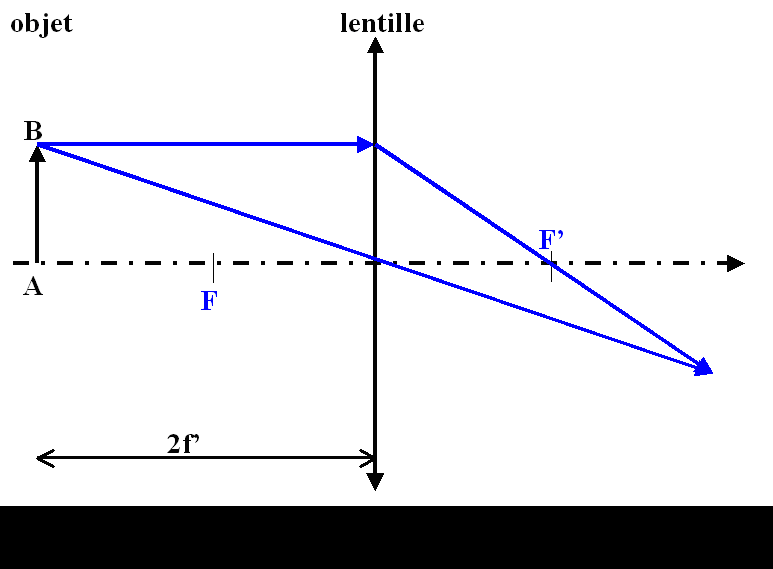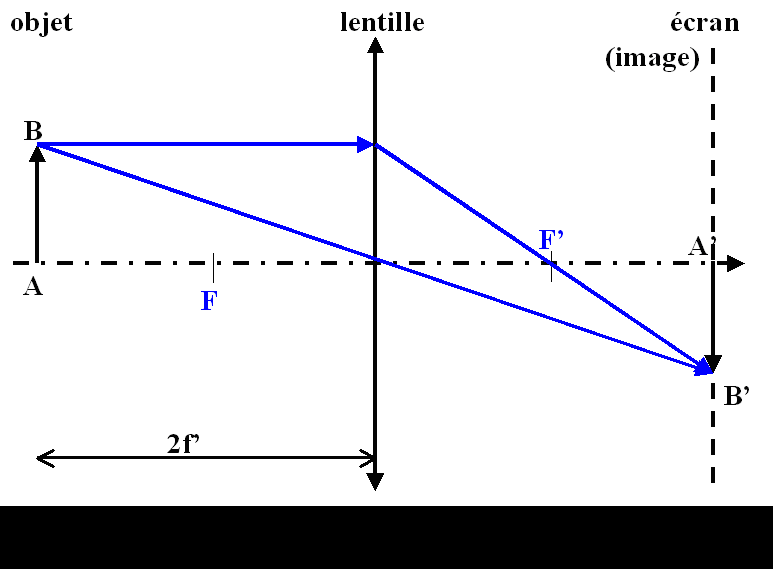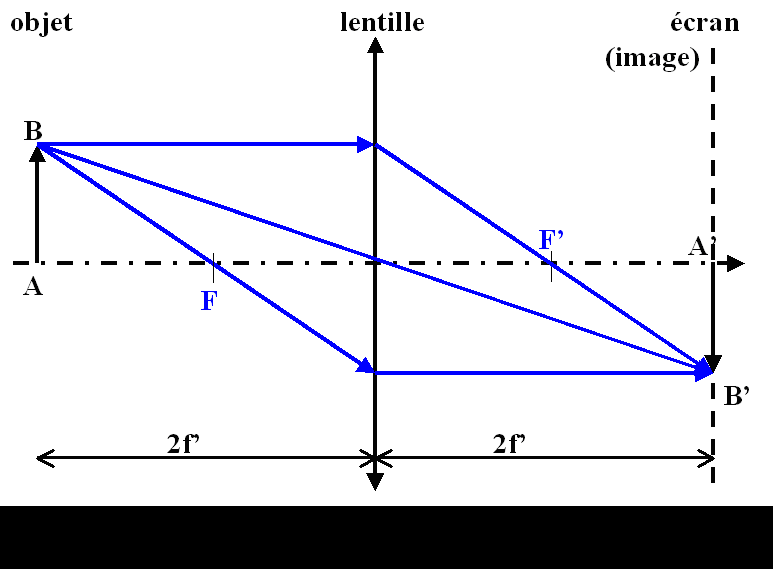
L'image et l'objet ont alors la même taille, l'image étant renversée.

Schéma animé sur la méthode de Silbermann

Formules de conjugaison

Les formules de conjugaison de Descartes donnent une relation entre les positions sur l'axe optique d'un objet A et de son image A'comparé au centre optique O. Elles sont exprimées avec des distances algébriques.

Soit A un point de l'axe optique et A'son image par la lentille :

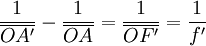
$\frac{1}{\overline{OA'}}- \frac{1}{\overline{OA}}=\frac{1}{\overline{OF'}}=\frac{1}{f'}$

Montage 2f-2f

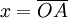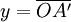On pose $x=\overline{OA}$ et $y=\overline{OA'}$ , par conséquent la formule de conjugaison devient :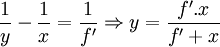 $\frac{1}{y}- \frac{1}{x}=\frac{1}{f'} \Rightarrow y=\frac{f'.x}{f'+x}$

Si $x = - 2. f'=$ alors $y = 2. f'$ (on parle pour cela de montage 2f-2f).

Ainsi, la distance objet-écran est 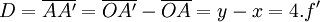$D=\overline{AA'}=\overline{OA'}-\overline{OA} =y-x=4ð$

Comparaison avec la méthode de Bessel

Cette distance D est la distance minimale qui existe entre un objet et son image, et la méthode de Silbermann apparaît alors comme un cas spécifique de la méthode de Bessel, celui où la position de la lentille est unique.

Bien que plus simple à comprendre que la méthode de Bessel, la méthode de Silbermann est plus compliquée à mettre en œuvre techniquement. En pratique, il faut opérer par tâtonnements en déplaçant la lentille et l'écran jusqu'à obtenir sur l'écran une image nette de même grandeur que l'objet mais renversée.

Liens externes

Une vidéo explicative sur la méthode de Silbermann

Recherche sur Amazone (livres) :

Ce texte est issu de l'encyclopédie Wikipedia. Vous pouvez consulter sa version originale dans cette encyclopédie à l'adresse http://fr.wikipedia.org/wiki/M%C3%A9thode_de_Silbermann.
Voir la liste des contributeurs.
La version présentée ici à été extraite depuis cette source le 15/04/2009.
Ce texte est disponible sous les termes de la licence de documentation libre GNU (GFDL).
La liste des définitions proposées en tête de page est une sélection parmi les résultats obtenus à l'aide de la commande "define:" de Google.
Cette page fait partie du projet Wikibis.