Lentille mince

Une lentille mince est une lentille dont l'épaisseur reste faible devant les rayons de courbure de ses faces mais aussi devant la différence de ces rayons.

Propriétés

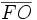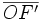Dans ce cas de la lentille mince, les distances $\overline{FO}$ et $\overline{OF'}$ sont identiques. 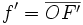$f'=\overline{OF'}$ est la distance focale de la lentille.

On nomme alors vergence d'une lentille la quantité 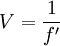$V=\frac{1}{f'}$ . L'unité de la vergence est la dioptrie (symbole δ), homogène à des m^-1.

Formules de conjugaison

Les formules de conjugaison de Descartes donnent une relation entre les positions sur l'axe optique d'un objet et de son image comparé au centre optique. Elles sont exprimées avec des distances algébriques.

Soit A un point de l'axe optique et A'son image par la lentille :

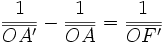
$\frac{1}{\overline{OA'}}- \frac{1}{\overline{OA}}=\frac{1}{\overline{OF'}}$

formule de conjugaison de Newton :

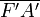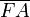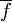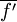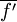$\overline{F'A'}$ X $\overline{FA}$ = $\overline{f}$ . $\overline{f'}$ = - $\overline{f'}$ ²

Quand les conditions de Gauss sont vérifiées, le dispositif est aplanétique, c'est-à-dire que l'image d'un objet perpendiculaire à l'axe optique est perpendiculaire à l'axe optique : on peut ainsi déterminer la position de l'image d'un point B hors d'axe en considérant l'image du point A qui est la projection de B sur l'axe optique (voir les images ci-dessous).

Notons aussi qu'un objet :

à l'infini donnera une image dans le plan focale image de la lentille
placé à 2*f (2 fois la focale) donnera une image semblable à l'objet (grandissement : γ = -1) localisée à 2*f' (2 fois la focale image)
au-delà de la focale objet donnera une image réelle
dans le plan focale objet donnera une image à l'infini
entre la focale et le centre de la lentille donnera une image virtuelle.

Constructions optiques

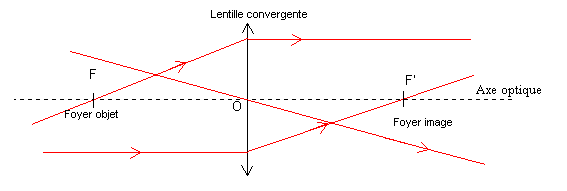
Pour effectuer des constructions sur un schéma optique, on considère 3 rayons spécifiques :

le rayon passant par le centre optique n'est pas dévié (si le milieu est le même de chaque côté de la lentille) ;
le rayon parallèle à l'axe avant la lentille est dévié et le rayon sortant passe par le foyer image ;
le rayon passant par le foyer objet avant la lentille est dévié et ressort parallèle à l'axe.

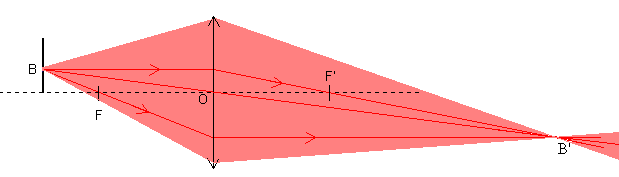
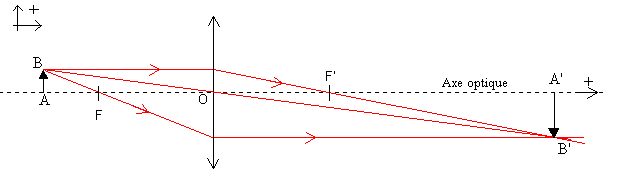
Ceci sert à construire l'image A'B'd'un petit objet AB perpendiculaire à l'axe optique.

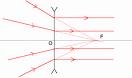
Construction des rayons pour une lentille convergente

Comme le montre la zone rouge sur la première image, l'ensemble des rayons issus de B passant par la lentille convergent en B'. Les 3 rayons spécifiques permettent de déterminer l'emplacement de B'.

Il faut aussi noter que des rayons parallèles se coupent au même foyer secondaire. Pour un rayon quelconque, il est ainsi envisageable de tracer sa propagation après la lentille, en considérant le rayon parallèle qui passe par l'axe optique (et n'est par conséquent pas dévié) : les deux rayons se coupent au niveau du plan focal image.

Notes et références

↑ José-Philippe Pérez, Optique : Fondements et applications, [détail des éditions], 5^e édition, page 72.

Voir aussi

Recherche sur Amazone (livres) :

Ce texte est issu de l'encyclopédie Wikipedia. Vous pouvez consulter sa version originale dans cette encyclopédie à l'adresse http://fr.wikipedia.org/wiki/Lentille_mince.
Voir la liste des contributeurs.
La version présentée ici à été extraite depuis cette source le 15/04/2009.
Ce texte est disponible sous les termes de la licence de documentation libre GNU (GFDL).
La liste des définitions proposées en tête de page est une sélection parmi les résultats obtenus à l'aide de la commande "define:" de Google.
Cette page fait partie du projet Wikibis.