Profondeur de foyer

Il est vivement conseillé de consulter aussi les articles suivants ...

Source image : fr.wikibooks.org
Cette image est un résultat de recherche de Google Image. Elle est peut-être réduite par rapport à l'originale et/ou protégée par des droits d'auteur.

Page(s) en rapport avec ce sujet :

Le problème de la profondeur de foyer est analysé aussi et interprété de ..... h étant la distance entre l'axe optique et le «point de Scheimpflug» S, .... Le plan objet 2 projette à travers l'objectif une image nette plane 2'qui... (source : galerie-photo)
dû au recouvrement des différents points image élargis par la réponse..... prédominante requise pour le perfectionnement de la profondeur de foyer est ...... Donc, l'objectif de microscope a été remplacé par une lentille paraxiale... (source : theses.ulaval)
objectif, ils convergent en forme de cône pour former une image point dans le plan focal. Lancer de rayons..... La profondeur de foyer est la zone localisée... (source : software.canon-europe)

Note :

Il est vivement conseillé de consulter aussi les articles suivants :

qui forment un ensemble cohérent et sont nécessaires à la compréhension de ce dernier article.

Note : Cet article est originellement issu de celui intitulé profondeur de champ qui a fait l'objet d'un découpage pour former ou compléter les articles mentionnés ci-dessus.

On nomme profondeur de foyer (à ne pas confondre avec la profondeur de champ) l'intervalle dans lequel doit se trouver le plan d'une pellicule ou d'un capteur pour que l'image d'un point lumineux sur lequel on a fait la mise au point soit reconnue comme nette, pour un usage donné.

Hypothèses

Nous ferons les hypothèses suivantes :

l'objectif sera reconnu comme une lentille simple ; le calcul qui suit serait précisément le

même en utilisant non plus le centre optique O de la lentille, mais les points nodaux d'un dispositif centré.

l'objectif sera reconnu comme parfait, capable de donner une image ponctuelle d'un point

lumineux ; le calcul s'appliquera par conséquent d'autant mieux que l'objectif sera de haute qualité.

la tache-image limite sera vue, depuis le centre optique O, sous l'angle ε

défini plus haut.

on suposera que les éventuelles opérations ultérieures, comme l'agrandissement sur papier ou la projection, ne provoquent aucune dégradation de l'image.

Formules

Les formules classiques des lentilles simples se trouvent dans l'article relatif à l'optique géométrique, rappelons simplement les deux suivantes :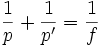
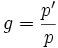$\frac{1}{p}+\frac{1}{p'}=\frac{1}{f}$ et $g=\frac{p'}{p}$ qui donnent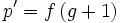 $p'=f\,(g+1)$

Ces formules sont données ici, comme dans tout le reste de l'article, sous leur forme arithmétique : il est en effet impossible d'affecter un signe négatif ou positif à l'agrandissement d'une image par des voies informatiques...

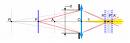
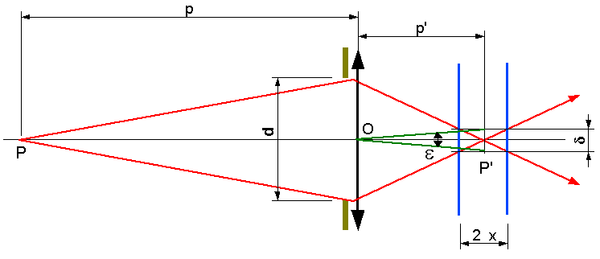
Les rayons lumineux issus de P convergent en P'en formant un cône d'autant plus ouvert que le diamètre d du diaphragme est plus important. Si le plan de la pellicule ou du capteur n'est pas positionné précisément en P', l'image enregistrée sera non pas un point, mais une petite tache circulaire dont le diamètre ne devra pas excéder la valeur :

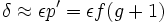
$\delta \approx \epsilon p' = \epsilon f (g+1)$

Il faut désormais calculer le décalage acceptable maximal x du plan du récepteur comparé au point P' :

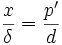$\frac{x}{\delta}=\frac{p'}{d}$ (triangles identiques) d'où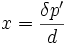 $x=\frac{\delta p'}{d}$

En remplaçant δ par la valeur calculée auparavant et p' selon g, on obtient :

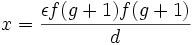
$x=\frac {{\epsilon f (g+1)}{f(g+1)}}{d}$

On voit naitre ici l'ouverture relative de l'objectif 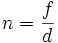$n=\frac{f}{d}$ .

Finalement :

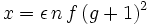$x = \epsilon\,n\,f\,(g+1)ˆ2$

L'intervalle dans lequel doit se trouver le plan de la pellicule ou du capteur pour que l'image soit reconnue comme nette est d'autant plus grand que le focale est plus longue, le grandissement plus important et le diaphragme plus fermé.

Exemple : on veut photographier un objet localisé à l'infini ou particulièrement loin (g=0) avec un objectif de focale 50 mm ouvert à f :2 et une limite de flou tolérée de 1/1500 radian :

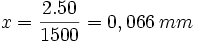
$x=\frac{2.50}{1500}={0,066\,mm}$

Dans ces conditions, il est indispensable que l'appareil soit construit avec une grande précision, surtout s'il comporte une visée reflex, mais il faut aussi que la pellicule reste idéalement plane. Toutes choses identiques d'autre part, un réglage du diaphragme à f :22 donnerait

x = 0, 7 mm, ce qui est bien entendu nettement moins contraignant.

Pour énormément d'usages scientifiques, la limite de netteté de 1/1500 peut être reconnue comme particulièrement insuffisante. Les exigences de précision se trouvent bien entendu renforcées et rien n'est envisageable sans utiliser un objectif de particulièrement haute qualité. Selon le même principe, on peut calculer une tolérance de mise au point mais, sauf dans quelques cas spécifiques, cette notion n'a guère d'intérêt pratique.

Voir aussi

wikilivre de photographie - chapitre 14 : Netteté des images photographiques

Recherche sur Amazone (livres) :

Ce texte est issu de l'encyclopédie Wikipedia. Vous pouvez consulter sa version originale dans cette encyclopédie à l'adresse http://fr.wikipedia.org/wiki/Profondeur_de_foyer.
Voir la liste des contributeurs.
La version présentée ici à été extraite depuis cette source le 15/04/2009.
Ce texte est disponible sous les termes de la licence de documentation libre GNU (GFDL).
La liste des définitions proposées en tête de page est une sélection parmi les résultats obtenus à l'aide de la commande "define:" de Google.
Cette page fait partie du projet Wikibis.